Senin, 27 September 2010

2210205023 Rotasi dengan pusat di A(a, b)


ROTASI TITIK DENGAN PUSAT A(a, b)
Oleh : Haryono
NRP : 2210205023




Prinsip Rotasi dengan pusat selain O(0,0) adalah beracuan pada Rotasi dengan pusat di titik O(0,0).
 
                                                             Gambar 1

Pada Gambar 1. titik P akan dirotasi sebesar α berlawanan arah jarum jam dengan pusat di A(a,b). Bayangannya adalah P’.
Rotasi titik P dengan pusat di A(a, b) sama artinya dengan A dan P ditranslasi sedemikian hingga titik A berimpit dengan 0(0,0). Titik P berpindah ke titik P1.  Seperti Gambar 2.
                                                                                Gambar 2                                                                              


Secara Matematis Koordinat P1 (x1, y1)
x1  = x – a
y1  = y – b
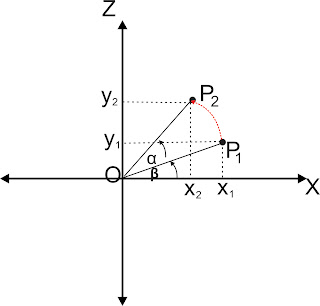
Selanjutnya P1 (x1, y1) dirotasi dengan sudut sebesar α P1 berpindah ke P2. Seperti pada gambar 3.
                                                                                 Gambar 3


Secara Matematis Koordinat P2 ( x2,y2)
x2  = r cos(α+β)
      = r cosαcosβ – r sinαsinβ
 x2 = (x-a)cosα – (y-b)sinα
y2  = r sin(α+β)
      =  r sinαcosβ + r cosαsinβ
y2  = (x-a)sinα – (y-b)cosα
Selanjutnya A dan P2 ( x2,y2) ditranslasi sedemikian hingga titik A kembali ke posisi semula dan titik P2 ( x2,y2) berpindah ke titik P’. Seperti gambar 4.
                                                                                    Gambar 4



Secara Matematis Koordinat P’(x’, y’)
x’  =  ((x-a)cosα – (y-b)sinα) + a
y’  =  ((x-a)sinα – (y-b)cosα) + b

Jadi Jika Titik P(x,y) dirotasi sebesar α dengan pusat di A(a,b), maka koordinat titik P dan P' adalah:
  P(x,y)  -------->  P'(((x-a)cosα – (y-b)sinα) + a,   ((x-a)sinα – (y-b)cosα) + b)



 
Diposting oleh di

2 komentar:

  1. Eko Mulyanto Yuniarno27 September 2010 pukul 16.45

    Transformasi matrix gabungan.
    Kasus pada gambar 1 dapat diselesaikan dengan menggunakan matrix gabungan.
    Misalkan Jarak 0,0 ke A adalah L1 dengan sudut beta, jarak A ke P adalah L2 dengan sudut alfa terhadap sumbu 0,0 ke A. Maka tempat kedudukan P dapat dihitung sebagai berikut.
    Bila Mr1 adalah matrix rotasi beta, MT1 adalah matrix translasi (L1,0) ,Mr2 adalah matrix rotasi alfa dan mt2 adalah matrix translasi (L2,0).
    P'= Mr1 . Mt1. Mr2. Mt2 .P(0,0)

    BalasHapus
  2. eriksoni1 Oktober 2010 pukul 07.31

    untuk kasus diatas misalkan
    titik P(x,y),A(a,b),P'(x',y') semua titik berpusat di titik O(0,0) jika panjang A dan P adalah R maka R = √(〖(x-a)〗^2+〖(y-b)〗^2 )dan sudut antara A dan P β maka β = invers tg ((y-b)/x-a) karena panjang jarak A dengan P' adalah sama dengan jarak A dengan P, dan sudut A dengan P'= α+β maka nilai x' = a + R cos(α+β)
    y' = b + R sin (α+β) sehingga titik P'((a + R cos(α+β)),(b + R sin (α+β)))

    BalasHapus

Langganan: Posting Komentar (Atom)