Senin, 27 September 2010
2210205014 - Terminologi dan Dasar 3D
2210205026 ( pemodelan3d sistem kini )
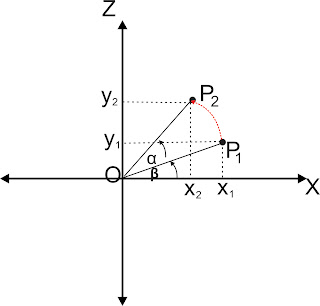
2210205023 Rotasi dengan pusat di A(a, b)
Jadi Jika Titik P(x,y) dirotasi sebesar α dengan pusat di A(a,b), maka koordinat titik P dan P' adalah:
P(x,y) --------> P'(((x-a)cosα – (y-b)sinα) + a, ((x-a)sinα – (y-b)cosα) + b)
Minggu, 26 September 2010
2210205022 - Proyeksi 3D
( 2210205024 ) Prinsip dasar 3D
2210205024 ( Prinsip dasar 3D )
SISTEM KOORDINAT PEMODELAN 3 DIMENSI
Sistem koordinat dua dimensi
Sistem koordinat Kartesius dalam dua dimensi umumnya didefinisikan dengan dua sumbu yang saling tegak lurus antara satu dengan yang lain, yang keduanya terletak pada satu bidang (bidang xy). Sumbu horizontal diberi label x, dan sumbu vertikal diberi label y.
Sedangkan Pada sistem koordinat tiga dimensi, ditambahkan sumbu yang lain yang sering diberi label z. Sumbu-sumbu tersebut ortogonal antara yang satu dengan yang lain. (Satu sumbu dengan sumbu lain saling tegak lurus).
Titik pertemuan antara kedua sumbu, dinamakan titik asal ( titik origin ), umumnya diberi label 0.
Gambar ( i )
Karena kedua sumbu bertegak lurus satu sama yang lain, bidang xy terbagi menjadi empat bagian yang disebut kuadran, yang pada Gambar ditandai dengan angka I, II, III, dan IV. keempat kuadran tersebut antara lain : kuadran I, kedua koordinat (x dan y) bernilai positif. Pada kuadran II, koordinat x bernilai negatif dan koordinat y bernilai positif. Pada kuadran III, kedua koordinat bernilai negatif, dan pada kuadran IV, koordinat x bernilai positif dan y negative.
System koordinat 3D
system koordinat Kartesius 3d, format umumnya adalah (x,y,z )
Gambar ( ii )
Melihat obyek secara tiga dimensi (3D) berarti melihat obyek dalam bentuk sesungguhnya. Penggambaran 3D akan lebih membantu memperjelas maksud dari rancangan obyek karena bentuk sesungguhnya dari obyek yang akan diciptakan divisualisasikan secara nyata. Penggambaran 3D merupakan pengembangan lebih lanjut dari penggambaran 2D.
Perbedaan antara obyek 2D dan 3D
Dalam 2D, obyek digambar dalam bidang xy
Gambar ( iii )
Dalam 3D, penggambaran dan penampilan obyek 3D bermain di didalam 3 ruas koordinat yaitu X, Y, dan Z.
Gambar ( iv )
Transformasi Objek 3D
1. rotasi
2. skala
3. translasi
Beberapa contoh transformasi obyek 3d
- Gambar 1
- Gambar 2
- Gambar 3
- Gambar 4
Sabtu, 25 September 2010
2210205025(Mengkonstruksi model model obyek 3d dengan metode ALGA BERKELAS)
| (Sebuah Pengalaman Pembelajaran Dalam Visualisasi Obyek Berdimensi Tiga) Abdullah NRM 2210205025 Pengantar Geometri merupakan mata pelajaran yang kaya akan materi yang dapat dipakai untuk memotivasi perhatian dan imajinasi murid-murid dari tingkat pendidikan dasar, menengah dan bahkan yang lebih tinggi lagi. Aktivitas-aktivitas dalam geometri informal di sekolah dapat digunakan untuk memperkenalkan ide-ide baru dan untuk memperkuat materi dan pengalaman belajar yang sudah diperoleh sebelumnya. Teorema-teorema tentang geometri di sekolah dapat di mulai dengan sesuatu yang konkrit, pengalaman memanipulasi yang memberi wawasan berguna dan pemahaman yang matang sebelum ada bukti yang terstruktur. . Salah satu paradigma pembelajaran yang kini sedang berkembang dan diterima luas oleh dunia pendidikan adalah Pembelajaran Kontekstual yang terkenal dengan konsep pembelajaran yang dihubungkan dengan kehidupan nyata atau yang sedang dialami atau yang pernah dilihat (real – life context). Selanjutnya sering kita sebagai pendidik lupa dan tidak menyadari bahwa kita selama ini sering terjebak pada pemikiran langsung atau tidak langsung telah mendoktrin pemikiran anak-anak bahwa ilmu-ilmu matematika itu serba ajaib, seba kebetulan dan serba sempurna. Upaya untuk mengimplementasi pemikiran tersebut salah satunya adalah mengoptimalkan aktivitas visualisasi obyek geometri agar memperingan atau mempermudah proses berfikir anak-anak dan membuat mereka fleksibel dan lebih kreatif. Apa Metode ALGA BERKELAS? Metode Alga Berkelas adalah suatu cara untuk mengkonstruksi model-model 3D yang dibuat dari bahan-bahan dari barang bekas (Pita kertas, Tusuk gigi, sedotan, kertas dan lain-lain) yang selanjutnya disebut Alat Peraga Berbahan Bekas disingkat ALGA BERKELAS. Metode ini dipergunakan untuk mevisualissasi obyek-obyek berdimensi 3.dalam proses pembelajaran . Salah satu tujuan metode ini adalah agar anak-anak senang membuat sendiri model-model 3D (Limas, Prisma, Balok, Kubus) yang sederhana sampai polihedron semi beraturan yang paling kompleks. Bagian ini mengilustrasikan bermacam-macam teknik yang mungkin dilakukan anak-anak dalam mengkonstruksi model-model 3D diantaranya adalah sebagai berikut : 1) Berbahan Baku dari Pita Kertas Potong beberapa pita kertas dengan panjang 12 cm dan lebar 6 cm. Lipat pita-pita tersebut dengan cara yang berbeda-beda untuk membentuk model sederhana dari bermacam-macam prisma. (GAMBAR 1) 2) Berbahan Baku Tusuk Gigi dan Sedotan Rekatkan tusuk gigi-tusuk gigi untuk membentuk rusuk dari sebuah limas atau gunakan potongan sedotan dan sambungkan ujung-ujungnya. (GAMBAR 2) 3) Jaring – jaring berbahan baku kertas Gambar yang rumit sering dibentuk pertama-tama dengan membuat jaring-jaring yang menunjukkan susunan sisi-sisi yang berdekatan. Potong sekeliling batas dan tandai rusuk-rusuk dibagian dalam agar dapat dilipat secara baik. Kemudian lipat dan rekatkan. Berikut jaring-jaring dari lima buah polihedron beraturan. Salah satu cara untuk menyalinnya adalah dengan memotong salinan dari bentuk dasar sisinya. Kemudian jaring-jaringnya disusun secara tepat dengan menandai setiap sudut dan sisi-sisinya. Satu kumpulan pola yang mungkin untuk mengkontruksi polihedron dapat dilihat pada gambar berikut ini. (GAMBAR 3) Keahlian yang diperlukan dalam mengkonstruksi secara hati-hati dan tepat benda-benda ruang ini sering diabaikan dalam proses pembelajaran matematika. Sebagai salah bentuk aktivitas hal ini dapat dilakukan. Akan tetapi pekerjaan dengan bangun ruang ini dapat membantu mengembangkan keahlian yang penting, yang juga sering diabaikan yaitu visualisasi berdimensi tiga. 4) Melipat Kertas Berbentuk Segienam Potong beberapa segienam beraturan dari kertas yang tebal. Lipat melalui ketiga diagonal utamanya dan gunting melalui salah satunya sampai ke pusat segienam. Setelah melipat segienam model-model limas segilima, persegi dan segitiga akan terbentuk. Jepitan kertas dapat digunakan untuk menjaga bentuk limasnya.(GAMBAR 4) Gunakan ketiga limas yang dibentuk untuk membantu murid-murid menemukan dan menggeneralisasi hubungan antara banyak titik sudut di alas dan banyak titik sudut dan rusuk. Limas dengan segi – n sebagai alasnya mempunyai n + 1 titik sudut dan 2n rusuk. 5) Melipat Kertas Berbentuk Lingkaran Guru sering mengkaitkan sebuah model dengan topik pada tingkat kelas tertentu. Akan tetapi kebanyakan model geometri mempunyai bermacam-macam aplikasi yang luas dari yang sederhana sampai yang menantang, dari sekolah dasar sampai sekioah menengah. Berikut akan disajikan gambar urutan pelipatan kertas berbentuk lingkaran menjadi tetrahedron terpotong. a) Persiapkan lingkaran dari kertas dengan jari-jari 20 cm b) Lipat dua diameter untuk mengetahui titik pusat lingkaran (GAMBAR 5) c) Pegang sisi dari lingkaran dan lipat ke belakang ke pusat lingkaran sebanyak tiga kali sedemikian hingga membentuk segitiga sama sisi.(GAMBAR 6) d) Lipat satu titik sudut ke titik tengah sisi di baliknya untuk membentuk sebuah trapesium sama kaki, dua titik sudut untuk membentuk belah ketupat, dan tiga titik sudut untuk membentuk segitiga sama sisi. (GAMBAR 7) e) Buka model ke atas sehingga keempat segitiga sama sisi membentuk sisi dari tetrahedron beratutan.(GAMBAR 8) f) Ketika Anda melipat setiap titik sudut dari segitiga yang besar ke titik pusat, akan terbentuk heksagon beraturan.(GAMBAR 9) g) Sekarang letakkan kertas yang dilipat dengan longgar di atas telapak tangan Anda. (GAMBAR 10) h) Masukkan ketiga penutup yang di atas besama-sama untuk membentuk sebuah model dari tetrahedron terpotong Ketika proses ini diperagakan oleh guru maka anak-anak di kebanyakan tingkat dapat mengikuti tahap-tahapnya dan membuat sendiri model-modelnya. Selamat Mencoba.... |
Jumat, 24 September 2010
(2210205021) Lebih Jauh Tentang Sistem Koordinat.
Perbedaan antara 2D dan 3D

- WCS ( world coordinate system ), wcs adalah koordinat yg posisidan arahnya selalu tetap dan bersifat absolute. Disini arah sumbu x,y,z yang anda masukan selalu dihitung dari titik acuan yang sama, tidak tergantung dari arah pandang saa ini.
- UCS ( user coordinate system ), ucs adalah sistem koordinat yang dapat diubah-ubah ( dipindah dan dirotasikan ) sesuai dengan keinginan pengguna.
Disamping 2 sistem koordinat tersebut sebenarnya ada lagi yang di sebut dengan koordinat polar dan koordinat relatif yang harus juga kita pahami juga.
- Relatif adalah sebuah koordinat pengguna untuk menentukan titik penempatan berikutnya dari titik saat ini, dengan memasukan nilai panjang dan lebar serta tinggi.
- Format relatif untuk 2D adalah @panjang, lebar
- Format relatif untuk 3D adalah @panjang,lebar,tinggi